[논문이야기] Interpretable Topic Analysis ③

[논문이야기] Interpretable Topic Analysis ②에서 이어집니다

이전 글에서는 GloVe를 본 연구의 핵심 워드 임베딩 기술로 사용하게 된 배경을 살펴보고, 나아가 그래프 표현을 통해 ‘토픽 내 단어간 관계’를 심도 깊게 반영하는 GTRF를 소개했습니다.

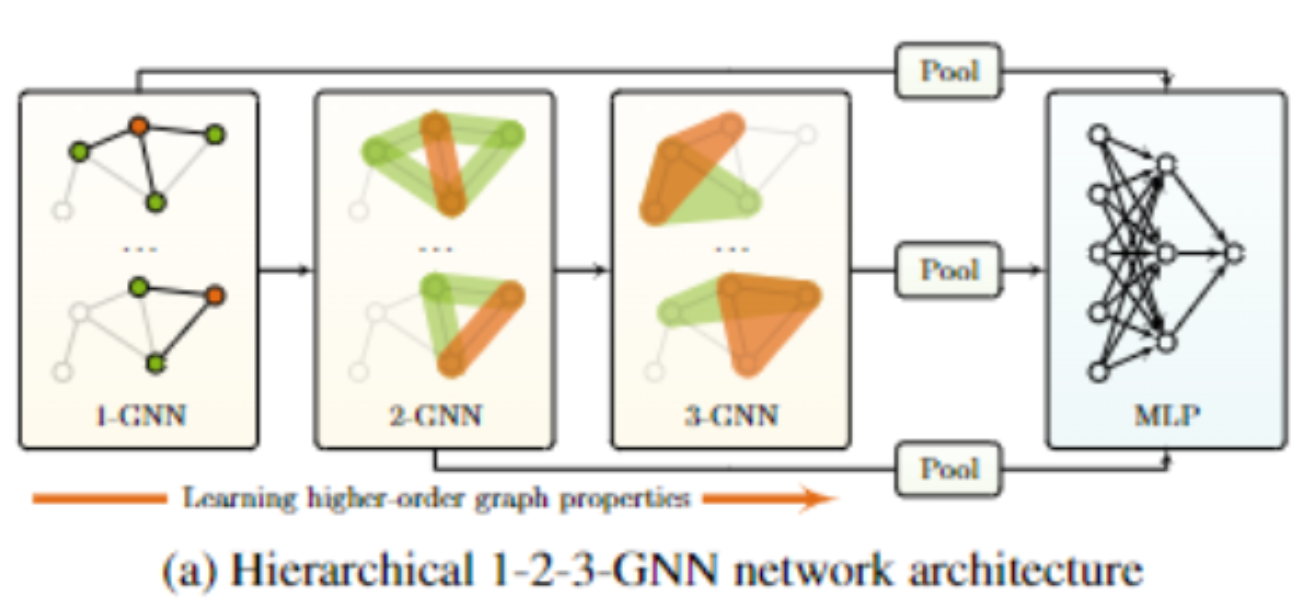
위 논의를 기반으로, 이번 글에서는 본 [논문이야기]의 핵심인 ‘GNTM(Graph Neural Topic Model)’를 살펴봅니다. GNTM은 higher order GNN(Graph Neural Network, 그래프 신경망)을 활용합니다. 즉, 위 그림처럼 GNTM은 order를 확장하면서 다양한 단어들의 연결 관계를 심층적으로 이해하고 임베딩할 수 있게 됩니다.

한편 GNTM은 NVI 계산을 통해 신경망 계산 비용을 상당히 개선할 수 있습니다.

Graph Neural Topic Model은 뭐가 다른 건데?

GNTM은 LDA에서 ‘그래프 구조’를 계산에 반영하는 과정을 하나 더 추가하는 한편, 학습을 효율적으로 하기 위해 변분 추론(Variational Inference, VI) 대신 신경망(Neural Network)을 이용한 신경망 변분 추론(Neural Variational Inference)를 활용합니다.

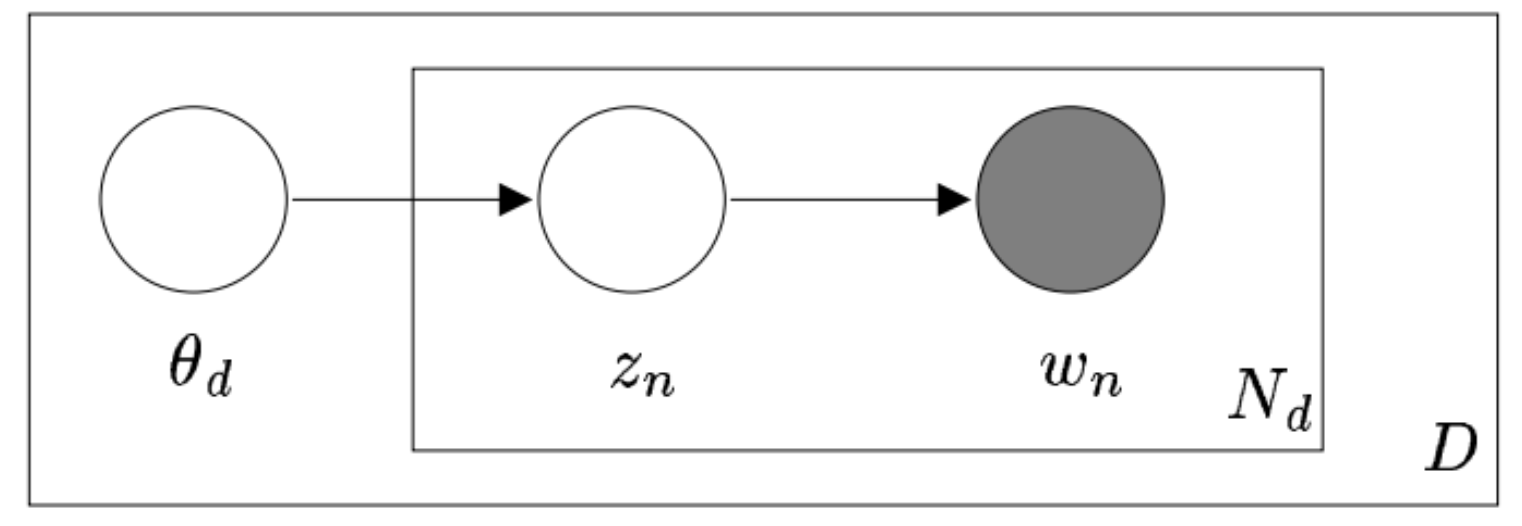
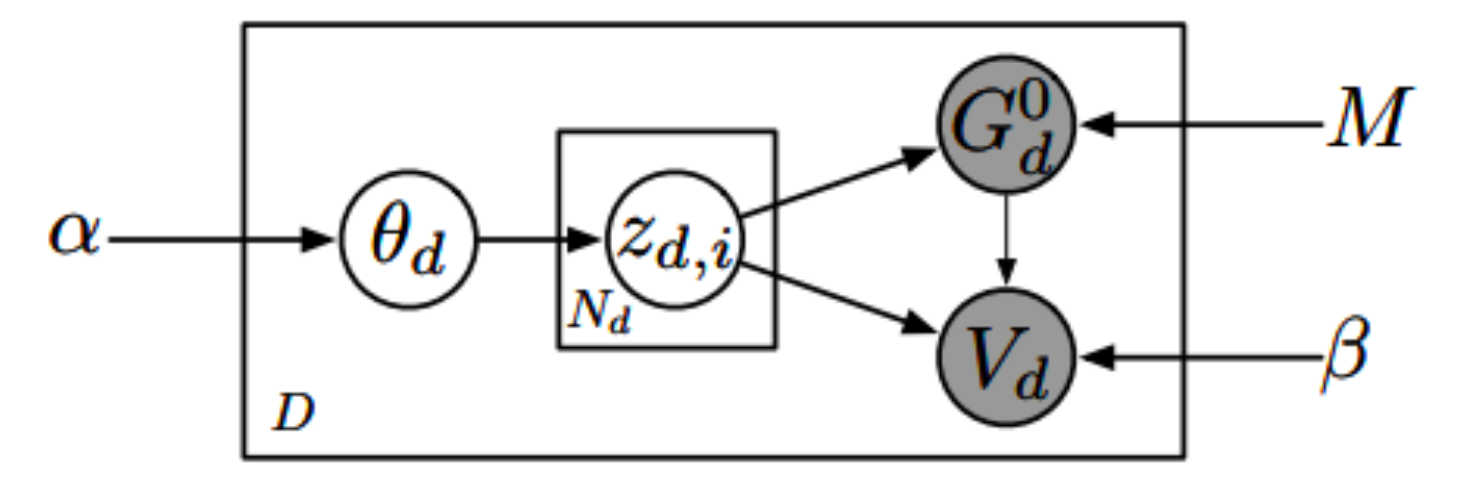
GNTM(GTRF)의 메커니즘을 살펴봅시다. 위 그림은 GTRF 계산을 LDA 계산과 함께 펼쳐놓은 것입니다. 이전 글에서 살펴봤듯, GTRF는 $\theta$가 정해졌을 때의 조건부 분포(conditional distribution)에 따라서 z의 구조가 달라지는 것을 학습하는 계산입니다.

어려울 수 있으니, 큰 틀에서 파악해봅시다. 먼저 문서 전체에 걸쳐 토픽들이 고루 퍼져 있다고 해봅시다. 이 때 토픽들이 차지하고 있는 비율은 각기 다를 것입니다. 이 비율을 나타내는 파라미터를 $\alpha$라고 해봅시다.

이 때 $\alpha$는 (LDA 접근 방법과 동일하게) 베타 분포(Beta distribution)의 확장 버전인 디리클레 분포(Dirichlet Distribution)의 형태를 결정하는 파라미터입니다. $\alpha$에 따라 분포의 모양은 아래와 같이 변하게 됩니다.

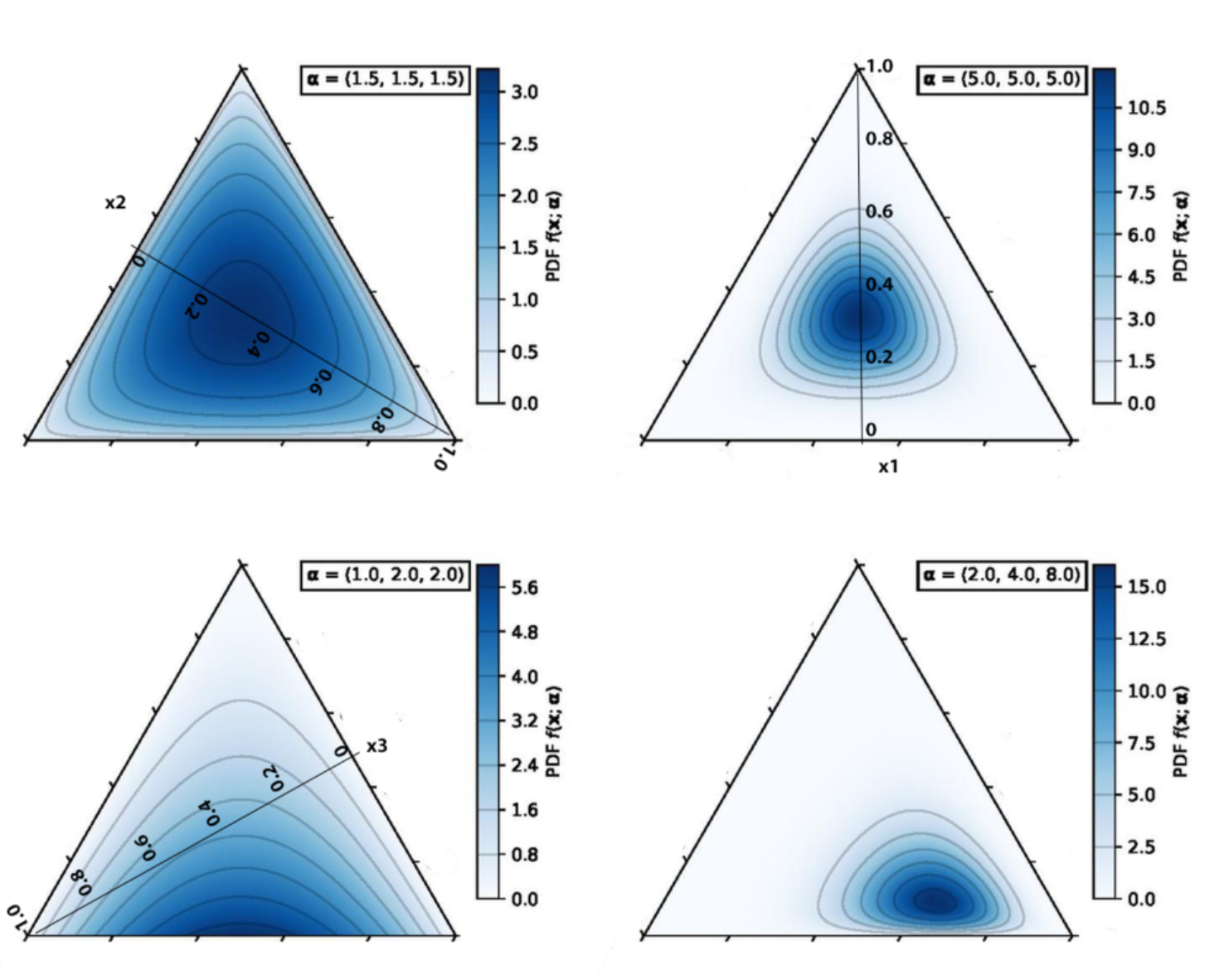
이렇게 해서 $\alpha$라는 파라미터로 토픽들의 비율이 정해지면 그 토픽들의 비율을 가지고 있는 파라미터 $\theta_d$라는 변수가 나오게 됩니다. 분포의 비율을 결정하는 것이지 경우의 수가 고정된 것이 아니기 때문입니다. 나아가 토픽 z가 결정이 되면 토픽에 따른 구조 $G$와 단어 셋 $V$가 결정이 됩니다.

GNTM의 차별점(1) : LDA에 그래프 구조 반영

지금까지의 논의를 통해, 우리가 가지고 있는 뉴스 정보들을 수치화하는 과정을 거쳤습니다. 이제부터는 어떻게 정확하고 빠르게 계산할 수 있을까?를 고민할 시간입니다.

처음은 매우 간단합니다. 디리클레 분포의 모든 파라미터($\alpha$)를 1로 설정해서 n차원에서 균등분포로 만듭니다. 현재 내가 기존에 가지고 있는 정보가 없으니 순수하게 토픽의 비율이 모두 동등하다고 가정하는 것입니다.

그 다음으로 토픽의 비율이 균등분포라는 가정 하에 랜덤하게 추출됩니다. 추출된 토픽의 비율에서 이제 토픽 z에 따라 또 랜덤으로 기사 문서 속에 있는 단어들의 토픽 배분이 결정 될 것입니다. 한편 중간 그래프 구조(graph structure)인 $G$는 어떤 구조가 숨어있는지 ‘학습’할 영역이기 때문에 모델링 처음부터 정의를 해줄 필요가 없습니다. 따라서 처음의 식은 아래와 같이 정리되겠습니다.

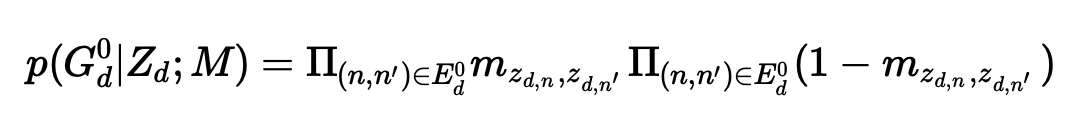
GTRF에서도 이미 확인했듯, 주어진 조건(여기서는 topic)에 따라 그래프 구조가 나올 확률이 다르며, 이를 나타내는 방법은 이항 분포의 분산 모양에서 확인할 수 있는 p(1-p)를 모두 곱하는 것입니다. 다시 말해 단어들한테 임의로 토픽을 할당하고, 그 할당 비율을 통해 m를 구할 수 있으며, 그 값을 통해 토픽들 간에 구조가 나올 확률을 이항 분포의 분산으로 수치화한다는 것이죠.

GNTM의 차별점(2) : NVI

마지막으로 살펴볼 부분은 NVI입니다. NVI는 텍스트 데이터 안에 있는 잠재 토픽의 사후 분포를 추정하는 방법입니다. NVI 알고리즘은 다양한 분포에 실제 사후 분포를 정확하게 추정하기 위해서 Neural Network 구조를 이용해 파라미터화합니다. 물론 그 과정에서 변분 추론(VI)에서 자주 사용하는 방법인 reparameterization (재파라미터화) 트릭으로 더 간단한 구조의 분포를 사용해 추정하기도 합니다. 신경망을 활용한다는 것은 적은 차원으로 축소해 데이터를 학습하는 VAE(Variational AutoEncoder)보다 다양한 분포에서 활용이 가능하다는 것을 의미하죠. 이는 보편적 근사 정리(Universal Approximation Theorem)을 바탕으로 모든 함수를 신경망으로 추정하는 것이 이론적으로 뒷받침 되기 때문입니다.

Reparameterization에 대해 부연하자면, 이는 기존의 확률 분포를 추론하는 과정에서 다른 분포로 대체해 학습 가능한 파라미터로 표현하는 것입니다. 이를 통해 역전파 계산이 가능해지고, 기울기를 효과적으로 계산할 수 있게 됩니다. 이 기법은 VAE에서 잠재 변수의 샘플링 과정에서 주료 사용됩니다.

앞서 언급했듯, NVI 뿐만 아니라 VI에서도 reparameterization trick을 사용합니다. 그러나 NVI만의 장점은 신경망을 통한 다양한 분포의 추정이 가능하면서도, 기존 디리클레 분포(Dirichlet Distribution) 기반의 하나의 정보만 활용 가능하던 VI와는 달리 로지스틱 정규 분포(Logistic Normal Distribution)를 활용해 평균과 공분산이라는 두 개의 정보를 활용할 수 있다는 것입니다. 나아가 NVI는 토픽 간의 구조를 추정하던 GTRF처럼 토픽 간의 관계에 대한 정보를 추론 하는 과정을 모델에 반영합니다.

[논문이야기] Interpretable Topic Analysis ④로 이어집니다