[논문이야기] 감염병 모델링 ②

[논문이야기] 감염병 모델링 ①에서 이어집니다.

이전 글에 이어 이번 글에서는 오류가 발생하는 다양한 상황에 따라 모델링 방법이 어떻게 달라져야 하는지 살펴보고, 나아가 구체적인 상황에서 각 모델마다 MLE 추정치가 어떻게 형성되는지 알아본다.

케이스 별 감염병 모델링 방법

이러한 오차의 특성을 고려해서, 다음과 같은 경우로 나눠서 감염병 모델링을 수행해 볼 수 있다.

case 1) 시스템 오차는 무시할 만한 수준인 반면, 관측 오차가 클 때: 임의의 새로운 사건은 관측값에 독립적으로 분포한다고 가정한다. 예컨대 포아송 분포(poisson distribution)에 따라, ‘감염자 수’는 t시간에 독립적으로 분포한다고 가정할 수 있다.

case 2) 시스템 오차가 보통 정도의 수준이며, 관측 오차가 큰 경우: 과하게 분산된 분포(overly dispersed distribution)을 사용해 추정한다. 예컨대 음이항분포(negative binomial distribution)를 활용해서 감염자 수를 모델링한다.

case 3) 시스템 오차가 크며, 관측 오차를 제외할 수 있는 경우: 이제는 시간 t와 t+1의 각각 감염자 발생 사건이 서로 독립적이지 않게 된다. 그러므로 모든 발생하는 사건들에 대해서 t사건이 주어졌을 때의 t+1 사건의 확률질량함수를 구해내야 한다.

case 4) 시스템 오차와 관측 오차 모두 크게 나타나는 경우: 이 경우 MLE로 파라미터를 추정하기 어려워지기 때문에 case 3으로 타협해야 한다. 그리고 이렇게 될 경우 MLE로 추정한 신뢰 구간(Confidence Interval)이 영향을 받게 될 수 밖에 없다.

시스템 오류는 무시할만한 수준, 관측 오류는 푸아송 분포일 때의 MLE

지금까지 논의한 ‘오차에 따른 모델링’을 좀 더 구체적으로 이해해본다는 차원에서, 시스템 오차가 무시할 만한 수준이며 관측 오차는 포아송 분포로 가정(case 1)하여 MLE 추정치를 살펴보자. 아래 그림의 위 그래프는 각 모델별 지수적 증가율(exponential growth rate)을, 아래 그래프는 각 모델별 주별 감염자수 곡선(epidemic curve)을 보여주고 있다.

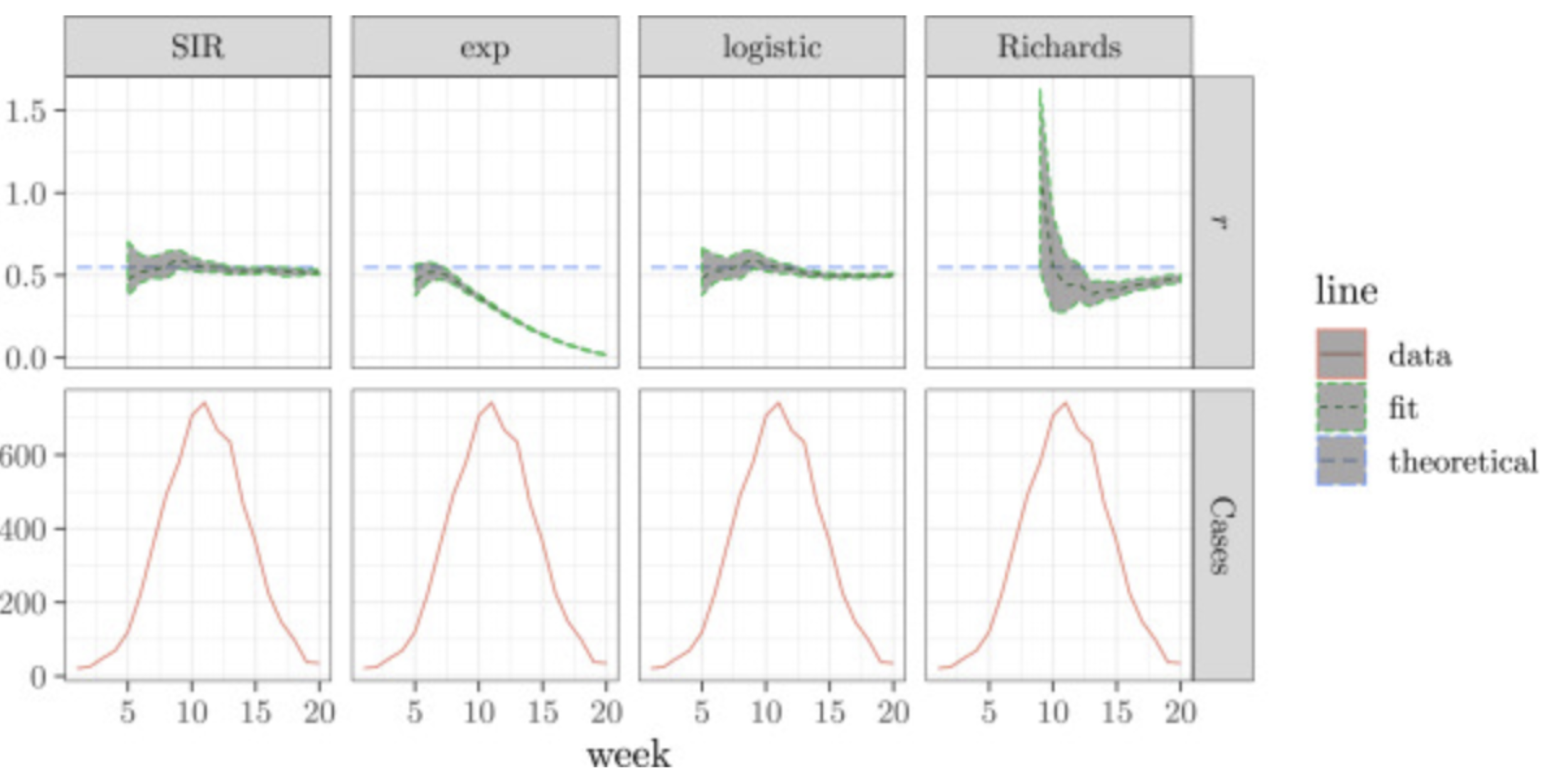
지수(exponential) 모델의 예측력(MLE)은 시간이 지날수록 빠르게 감소하는 것을 확인할 수 있다. 한편 logistic 모델과 Richards 모델은 유행병 최고조 시기(약 10주차 근방)에서 MLE 관점에서 높은 성능을 내고 있는 것을 확인할 수 있다. 마지막으로 SIR 모델은 모든 감염병 시기에서 일관적으로 양호한 예측력을 나타냈다. 한편 일간 데이터(daily data)를 사용하거나, 또 다른 구간 데이터를 사용한다면 결과가 달라질 수 있다는 점을 덧붙인다.

위에서 살펴봤던 것처럼, 오차를 어떻게 가정하느냐에 따라 추정 방법론은 다르게 적용된다. 그리고 각 오차 가정에 따라서 추정해야 하는 모델의 파라미터 숫자도 달라지게 된다. 심지어 파라미터의 수가 너무 많아지게 되면 자칫 오버피팅을 야기하게 될 수도 있다. 실제 위 그림 3의 결과에서도 나타났듯 비교적 파라미터를 많이 사용하는 SIR 모델과 logistic 모델은 신뢰 구간의 범위가 좁은 것을 확인할 수 있다. 신뢰 구간이 좁을수록 신뢰 수준이 낮다는 일반적인 상식을 고려하면, 적절한 모델링을 통해 파라미터의 수를 너무 크지 않게 조절하는 과정이 선행돼야 한다는 것을 알 수 있다.

실질 감염재생산 지수의 활용

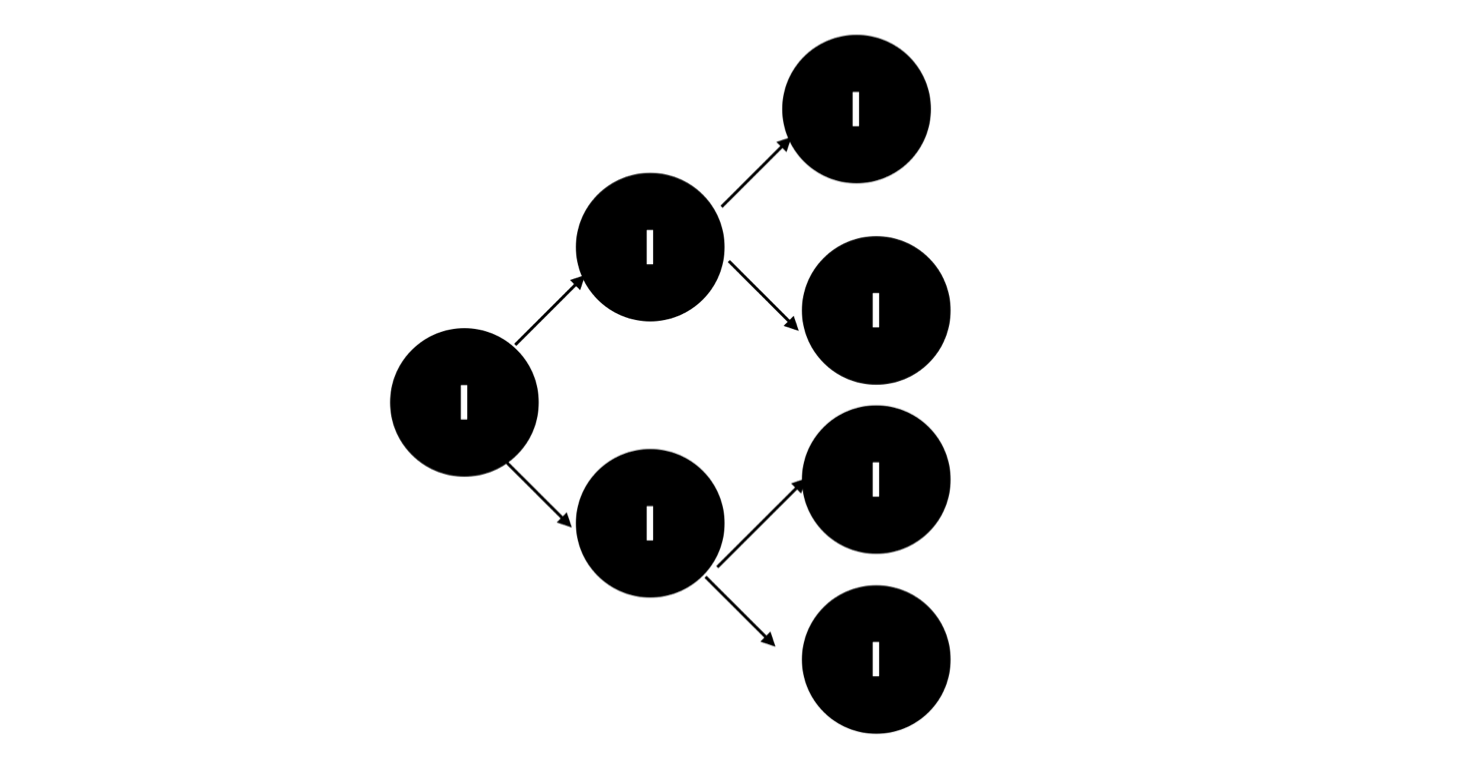
위 그림에서는 한 사람 당 두 사람씩 감염을 시켜 나가지만, 실제는 더 큰 수가 감염될 수 있다. 이 때 한 명의 환자가 평균적으로 감염시키는 환자 수를 ‘실질 재생산 지수’라고 한다. 이는 보건 업계에서 감염병의 확산 정도를 판단하는데 요긴하게 사용된다. 예컨대 R이 0보다 크면 감염이 늘어날 수 있는 상태가 되는 것이고, 0보다 작으면 감염전파가 소강상태에 접어드는 것으로 이해할 수 있다. 2003년 초 아시아에서 발생한 사스 바이러스의 R은 2~3이었다. 또 인간이 박멸한 유일한 감염병인 천연두는 감염될 수 있는 전체 인구 집단 안에서 R이 4~6이었다.

실질 감염재생산 지수는 위의 SIR 모델 또는 여타 현상학적 모델 등을 통해 다양하게 추정된다. 실질 재생산 지수는 $R_t = $(접촉자수 x 질병에 걸릴 확률) X (평균 감염기간) 으로 볼 수 있는데, 이 때 $R_t$를 구하는 방법론이 다양하다는 것이다.

데이터 생성 과정에 맞는 통계 모델 수립의 필요성

DGP(Data Generating Process, 데이터 생성 과정)에 맞게 통계적 모델을 수립하는 것은 매우 중요하다. 이는 감염병 모델링에서도 마찬가지다. 이와 관련해 필자는 앞서 오차의 종류에 따라 적절하게 모델을 구축해야 한다고 설명한 바 있다. 이 밖에도 데이터에서 발생하는 시스템 오차(process error)를 보정하기 위해 질병의 발생시간(generation time)을 질병의 증상이 발현된 시점으로 되돌리는 전처리 작업을 수행한 연구들도 몇몇(1,2) 존재한다.

앞서 소개한 방법론들은 공통적으로 최대가능우도추정법(Maximum Likelihood Estimation, MLE) 계산을 통해 실질 재생산 지수의 ‘신뢰 구간(confidence interval)’을 제시하고 있다. 여기에 추가적으로 MCMC(Markov Chain Monte Carlo) 시뮬레이션을 통해 실질 재생산 지수 값 변화에 따른 감염자 수 변화 추이 또한 살펴볼 수 있다. 아울러 연구자는 데이터의 초기 값을 버리거나, 모델에 다른 나라 데이터를 대입해보는 등의 민감도 분석(Sensitivity Analysis)을 수행함으로써 모델이 불확실한 현실상황을 다방면으로 설명하고 있는지 확인할 수 있다.

모델의 강건함을 위해서는

그러나 이같은 방법론들은 데이터가 충분한 상황에서만 의미가 있다. 만약 데이터가 부족하다면 모델이 질병에 대해 충분히 학습하지 못해 재감염 등의 사건에 대해 제대로 설명할 수 없게 될 수 있다. 또 다른 예로 코로나19와 같은 질병은 DNA가 아닌 RNA 종류에 속하기 때문에 바이러스 자체가 불안정하고 복제과정에서 돌연변이가 훨씬 자주 발생하게 된다. 이 경우도 마찬가지다. 충분히 다양한 질병 데이터를 모델에 인풋으로 넣지 않는다면, 모델이 코로나로 인한 감염자 수를 과소 또는 과대 예측하게 될 것이다.

어떤 효과가 종속 변수의 변화를 이끌어내는지 확인하는 ‘인과 추론(causal inference)’을 위해서는 변수 선택을 신중히 할 필요가 있다. 특정 변수에 대해 다른 요인을 통제한 부분 효과(partial effect)를 확인하는 것이 인과 추론의 핵심인데, 이를 위해서는 모델에 ‘적절한’ 변수가 ‘최대한 많이’ 포함돼야 하기 때문이다.

한편 나이, 성별, 지역에 따라 군집 분석(clustering analysis)를 수행한 대부분의 기존 감염병 연구들은 ‘슈퍼전파자’를 모델에 반영하지 못하는 한계가 있다. 슈퍼전파자란 다른 사람보다 더 많은 바이러스를 옮기는 사람을 지칭한다. 이들은 일반적으로 면역 체계가 망가져 고농도의 바이러스를 보유해 많은 사람에게 감염을 일으키게 된다. 즉 기존 연구 모델들은 감염병을 나이, 성별, 지역이라는 ‘단체’ 특성만을 기반으로 분석해왔기 때문에, 망가진 면역 체계 등의 ‘개개인의 특성’까지는 미처 반영하지 못했다는 것이다.

최근에는 슈퍼 전파자의 팩터를 찾기 위한 연구도 진행되고 있는 등 기존 연구의 한계를 극복하기 위해 많은 추가 연구들이 나오고 있다. 그러나 우리가 접하는 데이터는 개개인의 병력까지 가지고 있지 않는 만큼 완벽하게 감염병 모델링을 수행하는 것은 어려울 것으로 보인다.

그렇다면 기존의 모델링은 의미가 없는 것일까? 모델의 정확도를 끌어올리기 위해 어디까지 정교하게 만들 것인지, 복잡도는 얼마나 높일지 결정하는 것은 쉽지 않은 문제다. 비용을 천문학적으로 지불해 개개인의 병력을 모두 수집해 모델에 포함시킨다고 하더라도, 이는 자연 현상을 설명하는 일반화된 모델로서는 의미가 없게 될 것이기 때문이다. 이처럼 기존 연구들이 어느 정도 한계를 가지고 있는 것은 부정할 수 없는 사실이다. 그러나 기존 연구들이 실질 재생산 지수를 통해 최소한 어떤 정책에 신호를 줄 수 있다는 점에서는 유용한 모델인 것도 자명한 사실이다.